本文，将会从三个递进的层面和视角，一步步去发掘世界背后的运作规律、及其本质关联。

首先，探讨从0到1与从量变到质变的意义与内涵；接着，结合幂次法则去解读世界的本质发展规律；最后，则会上升到信息论的视角，去看待万物的关联性。

通过本文，或许我们能够发现，这个世界包括宇宙万物，其根本性的发展规律和路径——这或者可以说是在某个视角下的——第一原理。

第一原理（First Principle）——是一个最基本的命题或假设，不能被省略或删除，也不能被违反，相当于是在数学中的公理。而在物理中，是指从头计算，不需要任何参数，只需要一些基本的物理常量，就可以得到体系基态的基本性质。

主题目录如下：

• 从0到1与从1到N
• 从0到0
• 从量变到质变
• 幂次函数与指数函数
• 神奇的幂次法则
• 幂次量变与指数质变
• 幂次法则统治世界
• 非线性变化
• 信息论就是答案
• 结语
• 后记1：是的，就是循环
• 后记2：痕迹与自由
• 后记3：长尾理论与二八定律
• 后记4：素数与质变
• 后记5：预期寿命与概率分布
• 后记6：从数学解释幂次法则
• 后记7：复杂性涌现与层级封装
• 后记8：对数视角看幂律世界
• 后记9：从幂律到正态的熵增
• 后记10：非线性的边际

从0到1与从1到N

很明显，从0到1是——质变（从无到有），从1到N是——量变（从有到多）。质变——是性质改变，代表着翻天覆地的变化；而量变——没有性质改变，代表的仅仅是数量上的叠加。

这里要引出一个名词叫做——“质变点”，从0到1就是发生在质变点上的。

那么，通过量变的积累，就有可能抵达质变的结果，但这个过程是不确定的。就比如，有时候我们积累了很多的量变，但结果只是数量的叠加，始终也不见颠覆性的质变出现。

而这种不确定性，就呈现出了一些现象和规律，如：

• 努力是量变，努力不一定能成功，但是成功是质变，成功一定需要努力。
• 行动是量变，行动不一定有结果，但有结果是质变，结果一定需要行动。

从0到0

有了从0到1，就可以从1到N，是一个很自然的逻辑，并且可以想象：从0到1是要比从1到N，要困难的多的——甚至可以说难度不在一个数量级上。

例如，白手起家与继承家业，前者是从0到1，后者是从1到N。

然而在现实中，让人意想不到的是，在从0到1之前，还有一段路要走——那就是从0到0。

有时候，我们很努力，花了很多时间和精力，去计划一件事情、去做一件事情、去追求一件事情、去完成一件事件，但是结果却是收效甚微。这其中原因就在于，没有抵达质变点，所以就没有明显的效果。

事实上，我们的努力，都是在积累0，在没有遇到1之前，所有的努力都是0，所有的价值也几乎等于0。

虽然努力一定有其价值（包括失败的努力），但在没有获得1之前，所有的努力都是没有办法量化的（无法计算效用），并且我们也不知道努力与结果之间，究竟是什么样的关系——相关或不相关、 促成或阻碍。

所以，只要还没有获得那个1，一切努力的价值，就都是未知的不确定。而我们可以说——在获得1之前，一切都是0。

• **比如英语，**在进行了大量记忆之后，仍然无法轻松流畅地阅读。
• 比如写作，在进行了大量描写之后，仍然无法写出满意的文章。
• **比如绘画，**在进行了大量涂鸦之后，仍然无法呈现预期的作品。
• **比如编程，**在进行了大量实现之后，仍然无法得心应手地抽象。

这就是从0到0，再遇到1之前，无论做了多少都是微不足道的0，直到1的到来。天知道1什么时候才来，或是存不存在，但这就是从0到1的必经之路。

但从0到1的特别之处就在于：其过程并不是线性的量变，然后逐渐逼近结果，而是一种厚积薄发的——非线性质变。

因此，一旦获得了那个1，就会发现——英语找到母语感知、写作犹如上帝执手、绘画开启神来之笔、编程进入图灵模式——通常人们会说，这是突破了某个瓶颈，接着后面的每一步都更加的容易，成长会进入到飞速发展的阶段，仿佛一夜之间就变的和从前不一样了，获得了不可思议的力量。

此时，再回想从前，一切都是值得了，艰苦的过程和经历的所有磨难，仿佛都突然变成了时间所能兑换的奖励——并且过程越痛苦，成果就越美妙——这让过程成为最大的奖励，如同旅途就是回报。

甚至可以说，如果0是看不见的信息积累，那么1就是信息结构的呈现——这可以把真空变成虚场。

但需要注意的是：在有些情况下，无论进行多少量变积累，也一定无法得到正确的质变结果，即：无限量变等于质变。

• 例如，出现了原理性或规律性的底层错误**。**
• 例如，选择了一条“弯路”，质变需要的量变积累，超过了一个人所能提供的极限。
• 例如，所处的时代，无法提供必要的条件，即：历史进程并不准许。

从量变到质变

事实上，量变与质变相比，是极其微不足道的，因为质变是可以抵过所有量变总和的，但量变又是质变不可或缺的过程，这解释了很多道理或经验之谈，例如：

• 为什么失败，只会出现在彻底放弃之时？
• 为什么失败，是逼近成功的脚步？
• 为什么在快要放弃的时候，只要再坚持一下往往就是成功？
• 为什么有时候付出看不到回报，努力得不到收获？
• 为什么成功和失败如此接近，却又相差的十万八千里 ？
• ……

以上等等，都只需要再来一点量变，就有可能会产生质变，但如果选择放弃，就会彻底失去质变的机会，而质变就是翻天覆地的变化，可以抵消过去所有的失败，因此成败有时就在一念之差。

由此可见，失败就像是0，成功就像是1，从0到1——就像是从量变到质变的过程。而这个过程，就像齿轮——在惯性系中，最大的阻力会出现在最开始（即从0开始），但惯性（就像习惯与刻意练习）将会成就巅峰（即到1的质变）。

只不过，还需要多少量变，还需要坚持多久，还需要其它什么条件或因素，才能达成质变，我们并不知道。

但有一点是明确的：就是在0和1之间，隔着无数的000……000……还是000……，如果没有1，再多的0还是0，只有有了1，串联起积累的000，就是一次质变。

由此可见，1就站在质变点，似乎在向你微笑招手，并念着咒语：

• 它把所有的0，变得有意义。
• 它把看不见的0，变成触手可及。
• 它把万念俱灰的0，变成灿烂希望。
• 它把猴子，变成码农。
• 它把血溅山谷，变成小鹿溪水。
• 它把循环，变成递归，然后你才恍然大悟，原来出口一直就在自己身边，那么近又那么远。
• 它把黑洞，变成虫洞，把无法改变的历史，全部变成未来相互关联的剧情。
• 它把一切都看清，把拼图还原成一幅愿景，然后把你送到另外一个地方、一个阶段、一个层级，以及另一个世界。

那么，眼前的颅内模拟——全是000000……，请问它——1，在哪里呢 ？

事实上，量变与质变，还与我们的视角息息相关。

例如，我们看微观局部，往往看到的是量变，看宏观整体，往往看到的是质变。但量变与质变是那么的不同，会让我们根本搞不清楚，从微观到宏观，从局部到整体，是如何演变和发展的。

就像比尔·盖茨曾说过：“人们总是高估自己一年后能做的事情，却又低估自己十年后能做的事情。” ——这就是因为**“一年”往往并不能产生质变**，但**“十年”却又可以产生多次质变**。

类似的，人们也总是高估自己的能力，却又低估自己的潜力——这是因为能力是现在拥有的，而潜力是未来拥有的，两者之间间隔的就是若干次的质变。

可见，我们的偏好总是会——高估量变的速度，低估质变的结果。

那么，以上情况的共同点就在于，前半部分是自我认知偏差，即通常人们会高估自己低估别人，而后半部分是质变带来的信息鸿沟，这会让人脑在线性思维下的推理与预测——变得错弱不堪又形容虚设，堪比随机骰子。

换言之，由于量变引起质变，对细节局部的逐一了解，并不能对整体完全的把握，除非你能把所有的量变在脑海中——汇聚成质变。

而巴菲特与查理芒格的投资理念之一，即：坚持长期投注而非短期赌注。可以想象其中的原理，就在于长期回报是经过质变的结果，其收益会远远超过预期。

最后，需要强调的是——质变是可以抵过所有量变总和的，让我们用一个极端的例子，来说明质变的力量：

• 一个坏人一直做坏事，但做了一件**“质变级”的好事——比如拯救了100万人，结果这个坏人就可以质变**为好人。
• 一个好人一直做好事，但做了一件**“质变级”的坏事——比如毁灭了100万人，结果这个好人就可以质变**为坏人。

幂次函数与指数函数

在讨论幂次法则与量变质变之间的关系之前，我们需要了解一下幂次函数与指数函数。

首先，解释一下这个**“幂”字，在中文里它是指“遮盖巾”的意思。而在数学里，乘方的表达式，就是指数写在底数的头上，这如同遮盖了一个头巾一般，所以“幂”**——就是指乘方运算的结果。

例如，2的N次方，即N个2乘方运算的结果，也称为2的N次幂，或2的幂次方。

那么，幂数——就是幂结果的那个数字，也就是幂，同时也称为幂次，或**幂次方。**因此，在英文中——幂、幂数、幂次、幂次方，都称为——Power，即：代表巨大的力量或权利，显然这是乘方运算带来的效果。

在此，我们可以看到，幂的最终数值，其实取决于两个数，即：底数与指数，而这对应了两种变化——底数变化与指数变化。

对于底数变化，需要指数不变，如：1的2次方（1^2 ），2的2次方（2^2 ），3的2次方（3^2 ）等等，其形式是——f(x) = x^n，x是变量，n是常数（如2）。而这样的函数，就被称为——幂次函数，或幂函数。

例如，正方形面积的变化，是函数x^2中边长x决定的。

对于指数函数，需要指数变化，如：2的1次方（2^1 ），2的2次方（2^2 ），2的3次方（2^3 ）等等，其形式是——f(x) = n^x，x是变量，n是常数。而这样的函数，就被称为——指数函数。

例如，计算机内存容量的变化，是函数2^x中比特位x决定的。

那么，幂次函数对应的增长就是——幂次增长，指数函数对应的增长就是——指数增长，两者的关系在于：当自变量（底数与指数）很小的时候，幂次增长快于指数增长，但随着自变量不断增加，指数增长会远远超越幂次增长，并呈现出“爆炸性”的膨胀。

例如，幂次函数x^2与指数函数2^x，当x = -1时是1对0.5，当x = 2时两者相等，当x = 10时是100对1024，当x = 20时是400对1,048,576。

显然，由于指数增长这种“爆炸性”，在现实中它并不能维持很长时间（如复利效应，就是一种指数增长），否则就会消耗掉难以想象的资源，相反幂次增长，则就可以维持更长的时间。

而在统计学中，有两种统计概率的分布现象，就是由带系数的幂次函数与指数函数来表示的，它们被称为——幂律分布（Power Law Distribution）与指数分布（Exponential Distribution）。

• 幂律分布公式：P(x) = cx^(-a)，c和a是常量（c > 0，a > 0）。
• 指数分布公式：P(x) = e^(-λx)，e和λ是常量（λ > 0 代表单位时间内事件发生概率）。

这两种分布图像的对比，如下（蓝色幂律分布，红色指数分布）：

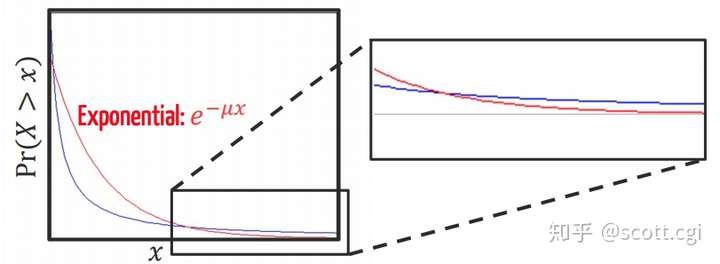蓝色幂律分布，红色指数分布

由图我们可以看出：

• 幂律分布的概率，在开始阶段高于指数分布。
• 幂律分布的概率，其衰减速度快于指数分布。
• 幂律分布的概率，在最后阶段高于指数分布。

可见，总体上相比指数分布，幂律分布衰减速度更快，但有更高的头部与更长的尾部。这正是说明了，幂律分布非常的不平均。

另外，还有一个隐藏的不同之处，就是幂律分布具有标度不变性（Scale Invariance），或称规模缩放不变性，即不同的幂律函数只是不同系数的标度缩放，其函数图像具有相似不变性，也就是说幂律分布具有分形特性。

在数学上，分形图形的基本特征，就是具有标度不变性，即：在不同的尺度下，分形图形具有自相似性，这是一种尺度上的对称性。这表明，分形图形具有与尺度无关的几何特性，即几何参数的不变性。

因此，在双对数坐标下，幂律分布是直线（负斜率）——具有缩放自相似性，而指数分布是曲线——没有缩放自相似性。

双对数坐标——指的是两个坐标轴的单位长度，都是经过对数计算后的平面坐标系，这意味着纵轴和横轴上刻度的增长倍数都是10。

神奇的幂次法则

幂次法则（Power Law）——是指事物的发展，其规模（如数量、大小、程度、频率等）与排名呈现幂次反比（幂次指常数次幂，如x^-1），又称之为**“幂律”**。

• 换言之，规模越小排名越高，规模越大排名越低；
• 或者说，决定性的大事件罕见，不重要的小事件众多；
• 或者说，改变世界的天才罕见，被世界改变的平庸众多；
• 或者说，高光时刻罕见，无聊时光众多。

以上等等，其内核就是——罕见的重要性与广泛的平凡性。

例如，规模x是人数，排名P(x)是财富，接着幂律分布函数选取（c = 100，a = 2）即：P(x) = 100x^-2，那么就能得出如下的，人数财富分布：

• P(1) = 100——人数规模是1，财富是100。
• P(5) = 4——人数规模是5，财富是4。
• P(10) = 1——人数规模是10，财富是1。

可见，大多数人获得少量财富，少数人获得大量财富，这就是二八定律的体现。

齐夫定律、幂律、帕累托定律之间的关系，参看： Zipf, Power-law, Pareto - a ranking tutorial

是的，幂次法则——指的就是幂律分布所呈现的结果，除了二八定律，与之相似的说法还有很多，如：长尾理论、马太效应、偏好依附、反馈增强、赢家通吃，等等。

这些在不同领域，不同的说法，体现的都是幂次法则，只不过它们的幂律系数不同，而它们都会呈现出，如下所示的幂律图像（绿色是头部，黄色是长尾）：

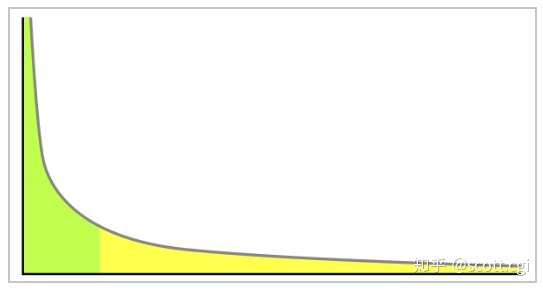绿色是头部，黄色是长尾

那么，在这个图像（头部罕见，尾部众多、快速衰减）背后，对应到现实世界的运作，其实就是——幂次变化，即：两个变量之间，呈现幂次比例关系。

幂次变化——就是指数不变，底数变化，如：x^2，x^-1，x取随机变量，指数为正就是正比例变化，指数为负就是反比例变化。注意：墨菲定律、复利效应、摩尔定律等——是指数变化。

事实上，根据经验和统计研究发现，幂律分布在我们的世界中是广泛且无所不在的，如：地震火山喷发规模、计算机文件大小、网页点击次数、论文及引用数、语言单词频率、人名姓氏使用、演化分支数量、神经活动规模、网络粉丝数、评论点赞数、文明强弱、月坑直径大小、行星间碎片大小、暗物质与暗能量占比，以及等等。

显然，幂律分布都体现了**“强者越强，弱者越弱，中庸难存”，即：赢家通吃的局面——而这就是幂次变化带来的非线性**效果。

在此需要特别指出的是：幂律由于存在分形特性，因此所有的幂律分布都是“嵌套”存在的。

例如，在二八定律中，20%的人掌握了80%的财富，那在这20%里仍然是20%对80%，即：4%的人掌握了64%（20% * 20% | 80% * 80%），0.8%的人掌握了51.2%（4% * 20% | 64% * 80%）等等，以此类推。

而硅谷著名投资人——彼得·蒂尔，在**《从0到1》中有这样一句，极具创造力的断言，即：“幂次法则，是宇宙的法则，是宇宙最强大的力量。”**

之所以，幂次法则的名字是——“Power Law”，就是因为指数方程描述的，是最不平均的分配，而核能中的链式反应，就是用指数方程推演的力量。

可以说，这个洞见本身，就像从0到1一样，有着质变的顿悟性与启发性。

那么，把幂次法则上升到宇宙的本质层面，这个视角有什么重要意义呢？

但在探讨这个视角之前，让我们先结合前文的量变与质变，来看一下指数变化和幂次变化之间的关系。

幂次量变与指数质变

从量变到质变，就是从0到1，中间隔着的就是——积累，而质变是可以抵过所有量变总和的。

那么，深入思考，我们就会有两个疑问，即：量变积累是如何抵达质变的？以及质变为什么会超越所有的量变之和？

这就是，幂次变化与质变变化登场的时刻。

首先说结论，量变——就是幂次变化，质变——就是指数变化，即：幂次量变积累出指数质变。

接下来，我们就用这个结论，来回答上面的两个疑问。

第一个问题，要搞清楚量变到质变的积累过程，需要回忆一下，幂次函数与指数函数，它们的形式分别是：x^2与2^x（假定系数常量为2）。

那么，如前文所述，这两个函数的关系，有三个阶段，如下：

• 第一阶段，在变量x较小的时候，幂次增长大于等于指数增长。
• 第二阶段，在变量x超过某个临界值的时候，幂次增长小于指数增长，并逐渐拉开差距。
• 第三阶段，在变量x越来越大的时候，指数增长出现**“爆炸性”膨胀，幂次增长“望尘莫及”**。

由此可见，在第一阶段——我们很容易通过幂次量变，来抵达指数质变；在第二阶段，我们需要更多的幂次量变，才能抵达指数质变；而在第三阶段，无论多少幂次量变，都无法再获得指数质变。

显然，从整体来看，我们会发现对于幂次增长——改变底数x是比较容易的，而对于指数增长——改变指数x是越来越困难的，直到变成不可能。

也正因为此，幂次增长就像是在量变，是我们可以一步步完成的积累，而量变积累抵达质变，其实就是幂次增长与指数增长的“交点”。

那么，随着不断地抵达质变，就会来到无论怎么积累量变，也无法抵达质变的时刻，这就是幂次增长远远被指数增长甩在了“身后”的原因——这时候只有通过切换幂次常数，比如由x^2切换到x^6去追赶2^x，才能继续抵达指数增长，从而继续产生质变效应。

而我们可以把——切换幂次常数，看成诸如：格局的跳变、圈子的转换、轨道的跃迁、领域的开辟、边界的突破、环境的巨变，等等。

总之，这是**“赛道”的切换效应，其对应着突破“层级封装”**的涌现现象——例如，原子核就是一种（动力学）层级封装，而突破这个层级，就是核能的涌现。

于是，再结合从0到1与从1到N来看：

• 量变——就是底数从1到N的幂次变化。
• 质变——就是指数从0到1的指数变化（即幂次常数的变化）。

第二个问题，说质变可以抵过所有的量变总和，其实就是说，指数增长是可以抵过所有幂次增长的总和。

显然，指数增长的“爆炸性”，从数学上就已经证明了这一点，即：每次指数级变化，都是对过去所有积累的**“翻倍”**，如2^2 = 4到2^3 = 8到2^4 = 16。

相比较，幂次增长，只是对过去积累的“非倍数”增量，如2 * 2 = 4到3 * 3 = 9到4 * 4 = 16，所以幂次增长是——量变。但需要注意的是，在开始阶段，我们总是很容易，通过幂次量变来抵达指数质变的。

不过，幂次增长的力量，在于其规模大小，因为从时间角度来看，单位时间的增长与当前的规模成正比，即：规模越大增长越快，且增长的时间固定不变。

例如，在x^2中x就是规模，那么从10到100，从100到1万，从1万到1亿，所用的时间是一样的。

然后，我们会发现，幂次量变积累所形成的结果——就是幂律分布。因为，如果量变积累是——幂次增长，那么积累完成度就是——系数除以幂次增长，而积累价值就是——系数除以积累完成度。

例如，量变积累是x^2，积累完成度是100 / x^2（系数为100），积累价值是100 / 完成度（系数为100）；那么积累2，完成度就是25，完成价值是4；如果积累10，完成度就只有1，完成价值就是100。

另外，幂律分布具有分形的自相似性，也就是说，无论是在局部还是整体，都是幂律分布的结果，即：强者越强（头部），弱者越弱（长尾），中庸难存（衰减）。

那为什么会这样呢？有三个方面的原因：

• 第一，幂次量变不断积累出指数质变，所以“高段”就会与“后段”远远拉开差距，形成头部。
• 第二，幂次量变在最初容易达成指数质变，所以“初段”不会绝迹，形成长尾。
• 第三，幂次量变到指数质变的难度不断增大，所以“中段”要么进入头部（拉开差距），要么进入尾部（被拉开差距）。

最后，需要注意的是，幂次变化与指数变化，都是非线性的变化，幂次量变可以在一定条件下**“捕获质变”，但会越来越难，直到如果不切换幂次常数**，就再也无法获得质变。

例如，获得了垄断，就是来到了幂律的**“头部”，也是幂次增长的极限，此后就很难再获得指数质变了**，除非切换**“赛道”（即幂次常数），从而开启一个新“幂次地图”**上的竞赛。

换个角度来说，指数级增长不可持续，否则某些重大的事件必须发生，即：切换赛道开启全新的幂次地图。

幂次法则统治世界

现在，让我们回到幂次法则的洞见：它是宇宙的本质规律。

这个视角的意义，就在于——所有事物的发展，都是非线性的幂次量变——这里的重点是两个关键词，即：所有事物和幂次量变。

第一，所有的事物，都在积累自己的量变，无一例外。

显然，质变就是我们所期待的巨大变革，但质变很难获得，需要付出超越我们心理预期的努力——因为人类的心理，对事物发展认知，倾向于正态分布和**线性反馈。**这种现实和心理预期的反差，也是让人们难于坚持和创新的——天生障碍和巨大困难。

正态分布（Normal Distribution）——又称**“高斯分布”（Gaussian Distribution），其曲线呈钟型，即两头低、中间高、左右对称，因此人们又经常称之为“钟形曲线”**。

而在质变之前，事物是处在一种竞争关系之下的，并且竞争从某种角度来看——就是零和游戏的博弈，是此消彼长的资源争夺。这会让人们没有时间和机会去思考，只是不断地跟着竞争对手，去做没创新的重复——从1到N。

那么，从0到1的质变，则会带来垄断——这是资源的总体增长，所有人都会在质变中获利，结果就是共赢，而整个社会和文明，也会因此得到发展和推动。

事实上，加班延长工作时间，是一种“低级压榨”——因为毫无效率和创造力，只是在堆重复的“数量”——从1到N，并且在这个“数量”中会塞入很多的“隐患”——各种Bug。

而“高级压榨”，是用最好的状态和创造力，去创造激动人心的结果——从而产生从0到1，这样的局面也会从零和游戏的博弈，转变成所有人都获利的共赢。

可见，低级剥削是在分蛋糕，高级剥削是在创造蛋糕——人类共同的敌人是本能，而不是智能——与其用本能去剥削智能，不如用智能去抑制和战胜本能（欲望让人追逐利润、无视他人利益）。

另外，虽然垄断会带来缺少竞争（即缺少压力源）的弊端，但过度竞争的危害更大，因为广泛存在参考点依赖的心理偏差，会让竞争不再向着有利共赢的局面发展。

参考点依赖——是指决策依赖于多个选项的比较，有点“两权其害取其轻”的意味，但这个过程的结果是往往是错配，因为比较让我们失去了“独立的理性判断”。

例如，孔雀的尾巴和麋鹿的大角，都是过度繁衍竞争的结果，这种竞争结果不利于个体及种群的整体生存（容易被捕食且耗费能量），仅仅是繁衍竞争过程中的失控或失调表现。

第二，幂次量变可以（在一定范围内）产生指数质变。

因此，在没有抵达指数质变的时候，就什么也不是——和前一个阶段差别不大，可一旦抵达质变点，就是一次指数级别——“陡峭曲线”的升级，即：指数增长。

而指数增长，带来的是超越之前所有积累之和的增长——这令人激动不已、又垂涎欲滴，并且还是改变世界和历史等一切轨迹的——根本驱动力。

那么，可以想象，在贫穷和财富之间，应该有一条基准线，即质变点。

当物质生活，越过这一条基准线，人们生活的满意度，就会极大的提高，创造力出现从0到1的质变——从而让产品质量和服务体验得到巨大的增强，无论是竞争还是合作都能形成正向循环，令社会整体和人均财富不断增加，人们生活的幸福感也会不断提高，结果就会更加激发人们的创造力。

显然，这是一个循环共赢的局面，呈现的就是幂次法则的“头部”。

相反，在基准线以下，人们在为基础物质生活条件而奔波——就会缺乏创造力、没有购买力、没有生产效率，只能重复从1到N，就无法提供更好的产品和服务，形成负向循环，社会财富就会变成零和游戏，人与人之间充满了你死我活的竞争和博弈，从而就会更加抑制和降低人们的创造力。

显然，这是一个循环齐输的局面，呈现的就是幂次法则的“长尾”。

可见，只有越过了这条物质基准线的质变点，一切才能有所发展——甚至不断地发展，一个人才有更多的上升机会和可能性。

第三，在物理上，质变就是相变，相变发生点就是临界点，而临界点附近的特性，可由幂次函数描述，其幂次就是临界指数（Critical Exponent）。

相变——就是从一种形式转化为另一种形式，就像水能以固体（冰）形式存在，也能以液体（液态水）和气体（蒸汽）形式存在，这些都是水的相。

换言之，从量变到质变，在质变点的物理特性，是服从幂次函数演化的，而实验表明，临界指数具有普适性，与具体的物理系统无关，即这是一个底层演化规律。

第四，幂次常数决定了，“幂次地图”或“赛道”之内的底层规律。

例如，很多宇宙规律，都是二阶平方的，如质能方程、波函数的概率，等等。

例如，在电磁相互作用中，电子交换光子方式的复杂程度，决定了其对相互作用强度的贡献，而这个贡献会随着光子的交换次数呈指数式下降，而这个指数的底，正好就是精细结构常数（近似1 / 137）——这即是一个幂次常数。

最后，我们在质变点，观察到的现象——就是涌现。

涌现——是指系统从低层次到高层次的发展过程中，一些特性不存在于低层系统中，却突然出现在了高层系统中。

简而言之，就是系统特性呈现出了，整体大于（甚至不同于）局部之和的现象。

• 例如，字词构成了句子——但句子整体的含义，比局部字词的含义之和更为丰富。
• 例如，细胞构成了人脑——但人脑整体的功能，比局部细胞的功能之和更为复杂。
• 例如，像素构成了图片——但图片整体的内涵，比局部像素的内涵之和更为多变。

那么显然，在涌现的过程中，必然存在着，从量变到质变的非线性变化，即从0到1。

事实上，局部之和也会小于整体，但这里没有涌现，例如：团队里都是“顶级专家”，结果相互不服，合作效率低下；爱下蛋的母鸡好斗，在一起不下蛋只打架；一个和尚有水喝，三个和尚没水喝。

非线性变化

如果幂次法则无处不在，那么就是从量变到质变的积累，无处不在。

• 比如癌症，就是突变积累，产生细胞质变。
• 比如顿悟，就是信息积累，产生思维质变。
• 比如灵感，就是思考积累，产生想法质变。
• 比如专家，就是训练积累，产生技艺质变。
• 比如，病毒传播、牙齿矫正、产品迭代、经济、战争、宗教、天气……

以上等等，都是幂次量变积累出指数质变的过程，而幂次变化与指数变化，都是非线性变化，而非线性变化，就是更为普遍的存在。

例如1，电池的电量衰减，不是匀速掉电，而是能够长时间维持在一个电量范围内，接着突然地快速掉电到极低的电量范围，也就是说，电池从可用到不可用是一个非线性的变化过程。

例如2，人的眼睛对光亮的敏感度，在不同的亮度下是不同的，也就是说，在黑夜中对光亮更敏感，在白昼中对光亮不敏感——这是一个非线性的感应过程。

例如3，感冒自愈，并不是平均每天好那么一点，直到完全康复，而是有三四天差不多程度的不适，然后突然好转，并迅速康复——这是一个非线性的变化过程。

例如4，用手指由远及近地遮蔽，单只眼睛前的一个物体，物体从可见到完全不可见的过程——这同样也是一个非线性的过程。

例如5，水果的售价，会在出现一点点变质之后，迅速地衰减到0，这显然是一个瞬间的非线性的变化过程。

例如6，在追求完美的过程中，达到了95%的完美之后，每一点提升，都需要非线性增长的资源与努力，甚至可能超越之前所有的付出之和。

事实上，我们身体的运作机制，包括伤口愈合、体力脑力的消耗与恢复，都是非线性变化的过程。甚至，衰老也是一个非线性的过程，即：我们不是慢慢变老，不是每天变老相同的程度，而是在生命最后的一段时间里，突然**（非线性）**变老。

可见，关于健康，我们可以保持很长——超越我们想象长的时间，直到最后健康突然（非线性）下降，并迅速死亡。至于现代社会，衰老与健康损耗的同时线性发展，则是“文明”带来的“负作用”。

而如果这个非线性变化发生在大脑里，就会让神经网络，快速形成结构化与抽象化的知识和认知——这就是学习。

而如果这个非线性变化发生在大脑外，就会让现实世界，快速按照我们的期望和想象去迭代与改进——这就是创造。

这里需要注意是，线性变化也可以进行量变积累，但质变是指数增长，所以线性变化是难以（甚至是无法）获得指数质变的。

那么试想，如果人类的学习与创造过程，是一个线性变化，那就可能永远也无法获得，学习能力与创造能力的质变增长，从而也就不会有今天的人类文明。

然后，我们会恍然发现，从受精卵到胚胎，细胞的分裂过程（1、2、4、6、8……）就是一个非线性变化，即：生长是一个非线性的增长现象。

例如，一个成年人，本质上就是婴儿非线性放大的版本，比较一下你身体的各个部位，与婴儿的各个部位，就会显而易见。

最后，我们甚至会发现——宇宙的进程、生命的进化、人类的诞生、文明的演进，统统都不是线性的。

例如，在宇宙大爆炸之初的10^-36秒，空间会以超级指数级的速度膨胀（暴胀理论，Inflation Theory），在10^-33秒之后以慢得多但仍然是指数级的速度，不断膨胀直至现在。

例如，如果把宇宙138亿年，当成地球一年的12个月来看待，那么生命会出现11月19日，人类会诞生于12月31日23点整，而文明会始于12月31日23点59分的最后一分钟。

例如，进化论（随机试错，适者留存）其实就表明，生物体随机到的微小差异，在自然的选择压力之下，经过非线性的长期积累作用，结果就会形成非常巨大的生存差异性——所以进化论又可以更形象地描述成：“物竞天择，适者有非线性差别的生存”。

于是，我们就要问了，为什么一切都是非线性的呢 ？

信息论就是答案

为什么非线性变化是世界的本质呢？在解释之前，让我们思考两个维度：

第一，当今世界，一个近在咫尺的非线性之物——就是计算机，其硬件的发展遵循摩尔定律，其软件的底层是2的幂次方，这两者都是非线性变化。

第二，现实世界的非线性变化无处不在，程序世界的非线性变化也无处不在，而在信息论的视角下，又有万物皆比特的信息观。

那么，整合到一起就是：构成世界的本质是信息，信息结构由比特构建，比特具有非线性变化规律，所以世界的本质到处透露着非线性变化。

有趣的是，从二进制的视角来看：

• 高位的从0到1——就是质变，并且抵过所有的低位之和，如：1000=8，0111=7。
• 低位的从1到N——就是量变，并且积累低位上1的数量就可以逼近质变，如：0111=7，1000=8。

可见，信息的指数变化，就会带来质变，而信息的指数变化，可能会来自连接数，即：信息传递的连接数，如：脑神经网络的连接数，带来的质变就是智能。

事实上，无论是幂次变化还是指数变化，它们都是乘方的形式，而2的幂次方就是最简单的乘方（即指数方程）形式。

于是可以想象，在乘方中，指数代表的就是概率轨道（范围），质变就是轨道（范围）的跃迁，底数代表的就是概率随机，量变就是随机的积累，而所有的非线性变化，都可以转换到2的幂次方来表达。

这么看来，计算机程序的世界，就像是真实世界的一个递归产物，而我们就有可能发展出用计算机去模拟一个世界的可能，并且那个我们模拟出的世界，又可以递归的创造计算机，继续模拟下一层的世界——就这么无限嵌套循环下去。

有趣的是，在游戏**《我的世界》**里，就有人创造了一个可以运行的计算机。

而强人工智能的发展，一旦出现人类智能级别的——机器智能，就宣告了我们只是上层世界的模拟，即：我们和我们的世界，都只是递归循环中的某一次迭代而已。

最后，事实上，现实世界的计算问题，都是指数增长的，虽然经典计算的存储是指数增长的，但计算过程却是线性增长的。于是，这就出现了经典计算机的线性计算能力，其实是跟不上现实的指数计算量的。

而量子计算，随着量子比特数量的增大，不仅存储会以更高阶的指数增长，还能够并行计算，从而实现应对现实问题的——指数增长计算。

结语

关于这个世界，我们得到了哪些结论：

第一，幂次量变积累出指数质变，是世界的本质规律。

也就是说，万物都在从量变积累到质变，但线性量变却无法积累出指数质变，因为增长速度不够，所以线性量变只能得到数量的叠加。

而有时候在宏观，我们看到的是指数增长，但此时在微观，我们没有注意到的却是幂次增长——也就是说，在指数变化的背后，必定充斥的是幂次变化。

那么，以系统的角度来看，任何系统量变都是幂次积累，因为任何系统都处在一个轨道之内（即概率范围内），而这个轨道（概率范围）就是系统的幂次常数。

第二，从0到1，是指数质变的表现，是我们的追求，也是被规律所推进的不可抗拒。

就像，一个市场可以超越其它总和、一个决策可以改变所有一切、一个创新可以颠覆所有、一次成功可以抵消所有失败、一次选择、一行代码、一个功能、一个特性、一个想法——可以决胜于千里之外。

这是什么？——这就是，我们称之为奇迹或是传奇，且不时会在我们的世界发生的——“质变点”。

**第三，**所有事物的发展，都有两个阶段：首先从0到1，然后从1到N，前者需要勇气、闪念、概率、突变与命运，而后者只需要——迭代。

从0到1是革命、是颠覆、是能量不守恒的混沌边缘、是新的平衡在黑暗中始作俑者般的膨胀。如果说0和1是猴子与人的区别，那么1和N就是平民和的富豪区别，我们可以说富豪和平民是平等的（因为质相同），但是我们不能说猴子和人是平等的（因为质不同）。

第四，在非线性变化中，一层套着一层，一端是无限大，一端是无限小。

我们的努力、我们的追求、我们的欲望、我们的经济、社会的发展、文明的进步、物种的进化、不断的探索——都只是曲线上的一个个点，我们做或不做，都是在积累00000，然后自愿或被迫的遇到1，升级到下一个阶段——没有尽头，一切都在无尽的循环迭代之中。

第五，我们的感受会随着时间变化，这是一种函数映射关系，而感受会操控想法，时间之流中会蕴含着诸多改变感受的要素——那么，这个函数或许就是一种，幂律分布。

所谓，人生的意义就是化学感受，想法随时间幂律分布，重要的是路径。

第六，幂次法则注定会让——“强者越强，弱者越弱”，那么换个角度就是——“成功是成功之母，失败是失败之父。”

第七，非线性变化会让——平均数预测失效。

因为，在非线性情况下，偏离正常值3个单位的情况，会比正常情况罕见300多倍，而偏离正常值5个单位的情况，则会比正常情况罕见100万倍以上。

换言之，用平均数（即线性思维）去评估预测非线性变化的波动性与可能性，是没有任何效用与意义的。

• 例如，不要因为一条河“平均”只有一米深，就试图趟过去，因为最深的区域可能会让你非常脆弱。
• 例如，某疾病的平均概率是万分之一，但具体到某个年龄段，可以是千分之一，甚至是百分之一。

关键在于，所有的小概率事件（如坠机），在差错面前都是非常脆弱的（如必死），但其概率往往都会被低估了一万倍以上（如黑天鹅）。

**第八，在二八定律视角下，**少数关键变量的计算，就可以大概率决定结果，想要极高的确定性，就要超多变量的计算。

第九，历史总是自相似地押着韵——这就是因为幂律的分形特性。

**最后，**毫无疑问，万物皆比特。

后记1：是的，就是循环

细细想来，我们一直不断地在努力积累000，并希望有一天可以遇到那个1，然后下一关、下一个阶段。可是或许下一关、下一个阶段，在得到之后——却是无尽的下一个关和下一个阶段。

这就像越过了高山的屏障，看到的是另一座高山，越过了沙漠，是另一片沙漠，来到了宇宙的边际，看到的是另一个宇宙，难道这就是量变到质变的无限循环？

是的——就是循环，是循环让量变积累成了质变，并重复从量变到质变的过程，这是一种“循环增强”模式（同回路增强、或闭环增强）。

这种模式，在宏观的效用，是让质变之后循环下一次质变；在微观的效用，是不断增强量变的积累，加速质变的过程，而这个过程本身依赖的也是循环。

例如，第一推动力——兴趣，会让我们在微观，循环练习积累量变，一旦获得宏观可见的质变，就会增强我们兴趣，从而促使我们更积极的循环练习，接着更快出现下一次质变，这又会再次增强我们的兴趣，然后又是循环练习，增强兴趣……就这么一直循环下去……

可见这个模式，就是微观循环的量变，产生质变，推动了微观循环本身，从而形成了宏观循环的质变，最终一个又一个循环的质变，得到的就是循环的增强，即：循环增强。

那么，这个模式——循环增强，其实是无处不在的，例如：

• 宗教中的马太效应，
• 竞争中的赢家通吃，
• 市场中的偏好依附，
• 发展中的积累效应，
• 商业中的规模效应，

等等，以上是幂次变化。

• 经济学中的复利效应，
• 心理学中的墨菲定律，
• 计算机中的摩尔定律，

等等，以上是指数变化。

而以上都是非线性变化的——循环增强，也可以称为——飞轮效应，因为这个过程具有滞后效应，就像飞轮加速一样，是一个从慢到快、再到越来越快的过程（但最后会抵达速度上限无法更快，除非换“轮子”）。

那么，在现实中，没人会在乎你的努力过程，人们只会认可你的成功结果，如果你不能脱颖而出，那么对别人来说，你就相当于从未努力过，或者觉得你再怎么努力，也都注定无法成功。

因此，我们应该铭记心中的一句话是：

人们只能看到你的（宏观）质变，但你不能否定自己的（微观）量变，而循环下去可以（变强）得到一切。

后记2：痕迹与自由

量变没有痕迹，质变会感到自由。

量变会遇到错误、会进展缓慢（甚至机器缓慢）、会想要从个人或是环境中找到原因与替罪羔羊，更重要的是，量变是漫长的，而如果一直处在**“量变无痕”**之中，我们就会充满情绪化、会怨天尤人、会自怨自怜，最终我们就会想要放弃。

但我们可以放弃吗？放弃了会怎样？

幂次法则告诉我们，量变无法避免，只有坚持走过量变无痕，才能抵达质变自由——是的，当我们来到质变点的时候，我们才能够真正体会到，那种突破以后的感觉，那是一种“自由”的感觉。

“自由”那是怎么样的感觉？——那是“自由”的感觉。

后记3：长尾理论与二八定律

长尾理论和二八定律都是幂次法则的体现，但为什么人们通常会认为，它们会是相对立的呢？

• 二八定律——认为20%的重要性超过了其它80%的总和，所以只要关注20%就可以了。
• 长尾理论——认为80%虽然不如20%的效果，但是只要时间够长，80%的收益可以和20%相媲美甚至超越，所以还是要关注80%。

这么看来，这两个规则确实对立的，一个强调20%重要，一个强调80%重要。但其中一个重要点就是时间——这个人类的头号敌人，也是人类最重要的朋友。

试想，如果给定一个时间范围，20%就会拥有绝对的领先优势。而如果不限定时间，这样80%在长尾里，获得了优势，我们也可以理解为——80%利用时间获得了质变。

可见，20%的作用，要么是直接获得了（80%积累产生的）质变，要么就是赢得了时间。

时间——其本身就是一个让积累，可以发酵成质变的关键变量。我们不能忽视时间变量，因为生命有限，80%的收益，结果需要100年的积累，而这100年就算一个人能活到，中间需要支付等待的成本，也都要算到收益损耗里——其损耗积累，则会产生负质变效应（如黑天鹅），从而抵消了长尾所带来的等待收益。

而从另一个角度来看，20%是关键，80%是细节，对于未知与创造，往往需要通过80%的细节路径，才能找到那20%的关键信息。

所以，长尾理论并不是否定了二八定律，而还是说明了——量变积累产生质变的过程。

后记4：素数与质变

素数，有着很简单的定义，即：一个大于1的自然数，除了1和它自身外，不能被其它自然数整除的数叫做——素数，否则称为——合数。

显然，0和1既不是素数也不是合数，而素数的特别之处，就在于它不能够分解成自然数（除了1和自身）的乘积，那么也就不能写成乘方（指数）形式。

可见，素数可以理解为——不是重复性积累的结果，而就像是积累出质变的结果。所以，素数在数学和物理现实中，都有着特殊的意义和作用——因为它是质变的节点。

或许，宇宙只需要0和1就足够了，后面都是0和1进行重复性积累，然后抵达一个个质变点的循环过程。

因而我们可以看到，历史数据揭示了概率，概率中隐藏着由幂次法则所主导的，可以抵得过所有历史量变总和的质变，而从量变到质变不确定的过程，则产生了黑天鹅与素数。

就如同二八定律，如果我们从素数的角度来看——其实是“1，1，3，5”的比例，那么20%中就有两个质变点，即：两个10%；而80%中，也有两个质变点，即：30%和50%。

这么理解的意义，就在于细粒度地刻画了，从量变到质变的过程，即是：

• 首先，要超过50%，就能得到第一次质变——获得明显优势。
• 接着，再超过30%，就能得到第二次质变——获得全面领先。
• 然后，再超过10%，就能得到第三次质变——获得极致结果。
• 最后，再超过10%，就能得到第四次质变——获得垄断局面。

或许，素数是一条路径，连接了宇宙的起点与终点。

后记5：预期寿命与概率分布

风险哲学家、随机性大师、“黑天鹅之父”——纳西姆·塔勒布**，在《反脆弱》**中，给出了这样一个表格：

• 正态分布——新事物比老事物，预期寿命更长，如：人类的寿命。
• 指数分布——新事物和老事物，预期寿命相同，如：物种的寿命。
• 幂律分布——老事物比新事物，预期寿命更长，如：基因的寿命。

事实上，对于正态分布（即高斯分布），预期寿命与已有年龄成反比，即：年龄越大，预期越少；而对于幂律分布，预期寿命与已有年龄成正比，即：年龄越大，预期越多。

例如，越古老的基因，越可能更长久的存在下去，而刚突变的基因，则还未经过时间的考验与环境的筛选——显然，基因的寿命存在“赢家通吃”的马太效应。

从此可以看出，幂律分布是**“自然选择，适者生存”**的结果，这里生存的时间越长，就越可以抽象为信息，从基因到分子原子到电子夸克，永恒不朽的是信息，而结构只是一个载体。

例如，技术很大程度上是一种信息，而不是一个实体，它不会像人类一样**“高斯衰老”，而是“幂律传播”**。

那么，结构的生存，其实只是反映了信息有限的生存状况，所以结构的寿命不一定是幂律分布。

后记6：从数学解释幂次法则

• 正态分布——是多个随机变量，独立相加的结果。
• 幂律分布——是多个随机变量，相互影响、相互关联、相互依赖的结果。

例如，“身高、智商”和寿命是正态分布（又称高斯分布），是因为“身高、智商和寿命”由多个独立因素控制，这些独立因素的效用之和决定了“身高、智商和寿命”。

那么，一个复杂系统，内部充满了相互紧密影响、关联、依赖的**“不独立”随机变量，这些变量之间远近不同的协调与作用，就会形成一个幂律分布的结果，而这种协调与作用，就是“自组织”**，典型的就是：生命系统、社会系统、金融系统、生态系统。

例如，在大脑的神经网络系统里，距离很近的神经元会同步放电——显然它们具有关联性——但随着神经元之间的距离增加，放电衰减呈现幂律分布——换言之，幂次法则在每个人的脑子里运作。

事实上，正是幂律分布要求随机变量之间具有关联性（即幂律关联），所以这样的系统才容易产生正反馈，正反馈容易积累量变，量变不断积累（在非线性系统中）容易获得质变，一次质变就可以超越之前的量变之和，因此会呈现局部之和大于整体的涌现现象。

例如，黑天鹅就是幂律分布的结果，也是量变到质变的结果，也是局部之和大于整体的结果，也是涌现现象。

那么，更宏观地来看，万事万物都是相互关联的，那么宇宙演化就会服从幂律分布，更抽象地来看，所有一切点点滴滴都是相互关联的，那么宏观与微观就会服从幂律分布，而这就是幂次法则主宰宇宙的原因所在。

例如，自然界随机演化的货币是能量，所以生物体的最优演化结果，是能量利用率（即能量消耗）最高，这和人类的文明活动高度一致，同理宇宙也是追随能量消耗（即熵增）演化的，所以生物演化的统计模型（如黏菌路网），可以应用到，从人类社会（如交通路网）到全宇宙（暗物质管道路网）。

后记7：复杂性涌现与层级封装

从某种角度说，**涌现 = 复杂性 + 能量，**即：在复杂性中积累出突破层级的能量就会涌现。

事实上，层级会阻隔相互作用、会压制混沌、会屏蔽复杂，会抵消随机——所以宏观通常都是极其确定的，其确定性就是来自层级的**“能量封装”**。

例如，原子是物质稳定的底层结构，就是因为原子核层，封装了核能（即动力学隔离），而量子效应无法出现在宏观，就是因为宏观层封装了微观的相互作用。

那么，无论是宏观整体控制微观局部，还是微观局部服从宏观整体，都在于层级封装了局部，接着层级之间的相互作用，就取代了局部之间的相互作用，即层级会阻隔微观的相互作用，并主导了秩序的演化，从而形成了更宏观统一的秩序。

因此，涌现现象，就可以理解为是层级封装被破坏之后的产物，即层级之间突破阻隔出现了更多的连接与相互作用，这对应到数学表达上，即：

在x^n中，底数x是层级内的变化，指数n是层级间的变化，如2^2切换到6^2——就是层级内的变化，而2^2切换到2^6（或2^-2到2^-6）——就是层级间的变化，也就是突破层级的涌现。

同理，在分形结构中，局部可以与整体自相似，但都是自相似，为何局部之和可以超越整体呢？

答案就是，突破层级封装的长程连接，带来了涌现效应——换言之，层级之间的长程连接与作用强度，就可以定量描述涌现的质变点。

那么或许，人脑的神经网络，正是由于遥远区域的长程连接与作用强度，才带来了智能的涌现，甚至是意识的涌现，而动物的大脑同样拥有神经网络，但缺少长程连接——即数量不够、层级不够、距离不够、连接不够——所以无法涌现出智能与意识。

有趣的是，如果说人脑中的长程连接带来了洞见，而洞见的洞见还是洞见，这是一种标度不变性，也就是自相似性，所以长程连接其实也是一种分形结构。

可见，**分形结构天生就具有涌现能力，**这说明，分形结构就是一种涌现动力学结构。

最后，在物理模型中，电磁力与引力都是“长程力”——它们可以在宏观宇宙中创造长程连接，而量子纠缠可以在微观宇宙中创造**“长程连接”**。

可见，从微观到宏观长程连接是无处不在的，可以说是长程连接主导了宇宙中的一切涌现，否则一切都将被封装在量子涨落之间。

后记8：对数视角看幂律世界

在双对数坐标系下，非线性关系的曲线就变成了直线——乘法变成了加法，除法变成了减法，倒数变成了正负，指数变成了乘数，根数变成了除数——这就是对数视角下的幂律世界。

那么，把非线性的曲线“拉成”线性直线之后，我们就会发现线性变化，其实是数量级的变化，我们感到了天翻地覆的变化，但这就是幂律世界的简单特性，即**“线性涌现”**。

而这条直线的斜率（固定比例），就是分形结构的维度，又称**“分形维数”（Fractal Dimension）——它是分形结构“褶皱度”的体现，其代表了规模缩放的不变性**，即不随规模和时间改变的比例。

可见，这个**“褶皱不变性”，就是幂律世界在不同维度上的复杂性与底层逻辑**。

后记9：从幂律到正态的熵增

物理学诺奖得主——肯尼斯·威尔逊（Kenneth Wilson），在收集研究了很多临界态的瞬变数据后，发现在临界态附近由无序到有序的相变过程中，关键数据指标都涌现了——幂律分布，如：水从液态相变成固态。

换言之，相互作用让无序相变成有序，同时也带来了幂律分布现象。

那么，从相互作用的角度来看，物质不独立，有可叠加积累的相互作用——就会呈现出幂律分布；相反物质独立，没有相互作用——就会呈现出正态分布。

事实上，没有任何相作用的系统（即全是独立变量），就是熵值最大的无序系统，而充满强烈相互作用的系统（即全是关联变量），就是熵值最小的有序系统。

可见，只要存在从无序到有序的熵减过程，幂律分布就会必然发生，而从有序到无序的熵增过程，即是由幂律分布趋向正态分布的过程。

而一个系统的演化，其实就是自身的熵减——所以演化系统必然会幂律分布，但熵减的代价是环境更加熵增——所以演化环境必然会正态分布。

因此，宇宙的熵增演化，最终将会走向正态分布的结局，但其过程将会历经各种幂律分布的“相变”，直到幂律曲线完全拟合成正态曲线。

后记10：非线性的边际

经济学是研究人、社会及世界运作的学科，而经济学中，最关心的就是——边际（Marginal），而平均和总量并不重要。

简单来说，边际就是微小的变化量，对应数学上的导数；通俗来说，边际就是新增带来的新增。

例如，成本的变化量（即新增产品的新增成本）就是边际成本，收益的变化量（即新增交易的新增收益）就是边际收益，产量的变化量（即新增制造的新增产量）就是边际产量，服务的变化量（即新增工作的新增服务）就是边际服务，效用的变化量（即新增付出的新增效用）就是边际效用。

例如，经济学不关心，一个人以前是好人还是坏人（平均意义），以及做过多少好事或坏事（总量意义），只关心一个人在环境变量发生变化时，其心理和行为会发生多少变化（边际意义）。

那么，经济学之所以可以通过边际（而不是平均和总量），来反映和预测人、社会及世界的运作，就是因为边际（即导数）可以抓住并体现万物底层的非线性变化（平均和总量则不行）。